MSI를 이용한 조합논리회로를 알아본다.
디코더.
디코더는 부호화된 입력을 받아서 부호화되지 않은 출력을 내보내는 복호화기라고 한다.
인코더는 10진 신호를 2진 신호로 변환한다. 이를 부호화기라고 한다.
디코더는 n 비트의 2진 코드를 최대 $$ 2^n $$개의 서로 다른 정보로 바꾸어주는 조합논리회로라고 할 수 있다.
즉 n개의 입력이 오면 $$ 2^n $$ 출력이 존재한다. 이를 보통 n X m 디코더라고 한다.
예를 들어 2 X 4 디코더를 예를 들자.
블록도.

진리표

출력으로 하나의 출력 값만 1을 가지고 나머지는 0을 갖는다.
내부회로도

회로도를 부울함수로 나타내면 최소항으로 표현할 수 있다.
결국 출력은 입력의 최소항을 의미하게 된다는 것이다.
이러한 디코드를 확장하기 위해선 작은 디코더를 여러 개 결합해서 필요한 크기의 디코더를 구성할 수 있다.
2개의 2X4 디코더를 이용하면 3X8 디코더를 구성할 수 있다.

입력이 3비트로 구성되었다고 할 때
입력의 두 비트는 두 디코더에 모두 연결된다.
최상위 비트 $$ A_2 $$에 따라 두 디코더 중 하나만 동작하게 된다.
디코더를 이용해 부울함수를 표현하면 최소항의 합으로 표현될 수 있다.
이를 쉽게 말하면 N개의 입력을 가진 N X $$ 2^n $$ 디코더와 M개의 출력을 가진 M개의 OR 게이트로 조합논리회로를 만들 수 있다.
예를 들어 F ( X, Y, Z) = $$ \sum m(1,3,4,7) $$ 를 디코더를 이용하여 구현한다고 하자.
주어진 부울함수는 3개의 입력과 8개의 최소항을 나타내기 때문에 3x8 디코더가 필요하다.
주어진 부울함수에서 최소항은 4개(1,3,4,7)이므로 이를 OR 게이트로 연결한다.

2023.02.27 - [도전] - BCD- 3초과 코드변환기
이전 시간에 알아본 BCD -3초과 코드 변환기의 논리회로를 다시 살펴보자.,
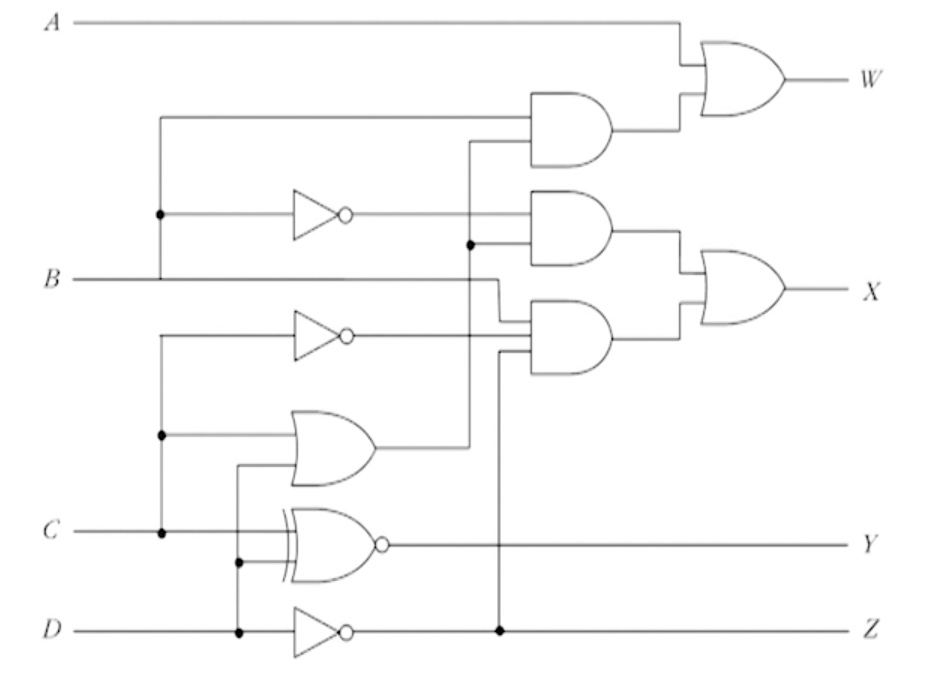
이를 MSI 디코더로 재구성할 수 있다.
4X16의 디코더를 사용하여 적절한 최소항만 있다면 동일한 기능을 하는 논리회로를 만들 수 있다.
AND, OR, NOT 게이트로도 회로를 만들 수 있지만 이미 만들어진 MSI 소자인 디코더를 통해 만들 수 있다는 것도 기억하자,.
멀티플렉서/ 디멀티플렉서.
멀티플렉서는 여러 개의 입력선 중에서 하나를 선택하여 단일의 출력을 내보내는 조합논리회로를 말한다.
예를 들어 CPU가 사용하는 여러 개의 레지스터가 존재하는 경우 이 중 하나의 레지스터를 선택하기 위해 멀티플렉서를 사용하기도 한다.
혹은 시스템 버스를 선택하는데 사용될 수 또 있다.
다만 특정 입력선을 선택하기 위해서는 선택변수를 사용해야 한다.
즉 $$ 2^n $$개의 입력선 중에서 특정 입력선을 선택하기 위해서는 n 개의 선택변수가 있어야 한다.
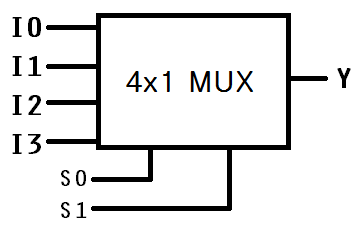
MUX라는 약어로 사용되기도 한다.

선택 변수에 의해 입력이 출력으로 전달된다.
만약 선택변수 C1, C2가 00 이면 X1의 AND 게이트 입력 값이 모두 1이 되어 출력이 1이 되는 반면에
나머지 X2, X3, X4의 AND 게이트 출력은 0이 된다.
따라서 OR 게이트로 입력되는 네 입력 중 X1이 입력된 AND 게이트의 출력만이 1이므로 결국 OR 게이트의 출력은 X1의 값이 된다.
멀티플렉서는 여러 개의 입력 중에서 하나를 선택하여 출력으로 내보내는 연산을 수행하기 때문에 데이터 선택기라고도 한다.
멀티플렉서는 OR 게이트르 가진 디코더와 같은 기능을 수행하게 된다. 따라서 멀티플렉서의 선택선으로 입력변수의 최소항을 선택할 수 있으며, 또한 입력선을 이용하여 이 최소항을 입력할 수 있다.
이는 n 개의 선택입력과 $$2^n$$ 개의 데이터 입력을 가진 멀티플렉서를 이용하면 n + 1 개의 변수를 가진 부울함수를 구현할 수 있다.
'도전' 카테고리의 다른 글
| DevOps 소프트웨어 개발 (0) | 2023.03.13 |
|---|---|
| 순서논리회로 (1) (0) | 2023.03.07 |
| 패리티 발생기/검사기 논리회로도 (0) | 2023.02.27 |
| BCD- 3초과 코드변환기 (0) | 2023.02.27 |
| 조합논리회로(1) (0) | 2023.02.26 |



댓글