object picking?
3D 물체를 마우스 클릭이나 터치와 같은 행동을 할 때 어떻게 이를 감지할까?
픽셀을 선택했다고 해도 이 픽셀이 어떤 3D 물체 것인지도 알 수 없다. 2차원에서는 힘들다.
그렇다면 3차원의 기하적인 추론을 통해 달성할 수 있지 않을까?
Z좌표가 없다고 하면 스크린 상에서 마우스 포인터의 좌표는 (x, y, 0) 일 것이다.
이때 우리는 ray를 한 번 고려해보자. 시작점이 있고 한쪽으로 무한하게 뻗어나가는 직선이다.
z 축 방향으로 모두 뻗어나간다고 할 때, ray의 정의는 시작점(x, y)과 direction vector(0,0,1)로 표현될 수 있지 않을까?
그럼 이 ray가 누구랑 부딪치는지 판별을 하면 되지 않을까?
근데 viewport에서 오브젝트에 대한 정보가 있나? 폴리곤 메시, 프레그먼트는 알 수 있어도 오브젝트에 대한 정보를 알 수 없을 것 같다.
screen space, clips space, camera space, world space, object space 이 중에서 해결방법이 있을 것이다.
screen space, clips space, camera space, world space에서 개별 object에 대한 정보는 없다. 이는 object space에서 각 space로 변환된 이후 space부터는 단일한 공간으로 취급되기 때문에 여러 오브젝트 간의 구별이 없다.
그렇기에 object space에서 ray와 만나는 모든 폴리곤 메시는 해당 object를 가리키기 때문에 object space가 어떠한 해답을 가지고 있을 것이다.
그러면 역으로 screen space에서 object space까지 다시 돌아가야하는데 어떤 변환을 해야 할 까?
카메라 좌표계의 절두체에는 4가지 속성이 있다. near, far, fov, aspect가 있다.
n, f는 카메라 절두체의 앞면까지의 거리와 뒷면까지의 거리였다.그리고 카메라좌표계에서는 -z 축으로 나타나고 있다.
이를 통해 start point를 카메라 공간의 ( x, y, -n)으로 치환할 수 있다.
이제 x, y의 값을 구하면 된다.
카메라 공간에서 clips 공간으로 변환할 때 projection transform을 이용했다.

그러면 카메라 공간에서 정의한 시작점에 projection matrix를 곱하면 clip 좌표가 나올 것이다.
Perspective division(원근 분할)은 3D 공간에서 호모지니어스 좌표계를 사용할 때 적용되는 연산입니다.
호모지니어스 좌표계에서는 점의 위치를 (X, Y, Z, w) 형태로 표현합니다.
여기서 w는 원점으로부터의 거리를 나타내는 값이며, w값이 작을수록 원점에 가깝다는 의미입니다.
Perspective projection(원근 투영)을 수행할 때, 3D 객체를 2D 화면으로 투영하려면, 호모지니어스 좌표계에서 (X, Y, Z, w)를 (x, y) 좌표로 변환해야 합니다. 이때, perspective division 연산이 수행됩니다.
Perspective division 연산은 (X, Y, Z, w) 좌표를 (X/w, Y/w, Z/w) 좌표로 변환하는 것을 말합니다.
이 과정은 3D 공간에서 원근 투영을 수행하면서, 원근에 의한 왜곡을 보정하기 위해 수행됩니다.
Perspective division 연산을 수행하면, w값이 작을수록 점의 위치가 화면에서 더 가까이 표시됩니다. 따라서, 이 연산을 통해 3D 객체를 올바르게 투영할 수 있습니다.
카메라 공간의 시작점은 그러면 다음과 같은 호모지니어스 좌표를 갖고 있다.
start point ( x, y, -n, 1) 이 좌표를 projection matrix와 곱한 결과의 w값은 아직 호모지니어스의 좌표를 표현하는 4차원 벡터가 나오고. 이를 perspective division을 수행하기 위해 각 좌표를 w로 나누면 NDC로 표현된 clip space의 시작점으로 옮겨지게 된다.
이렇게 나온 clip 공간의 좌표를 통해 viewport transform을 하면 screen space의 시작점이 나올 것이다.
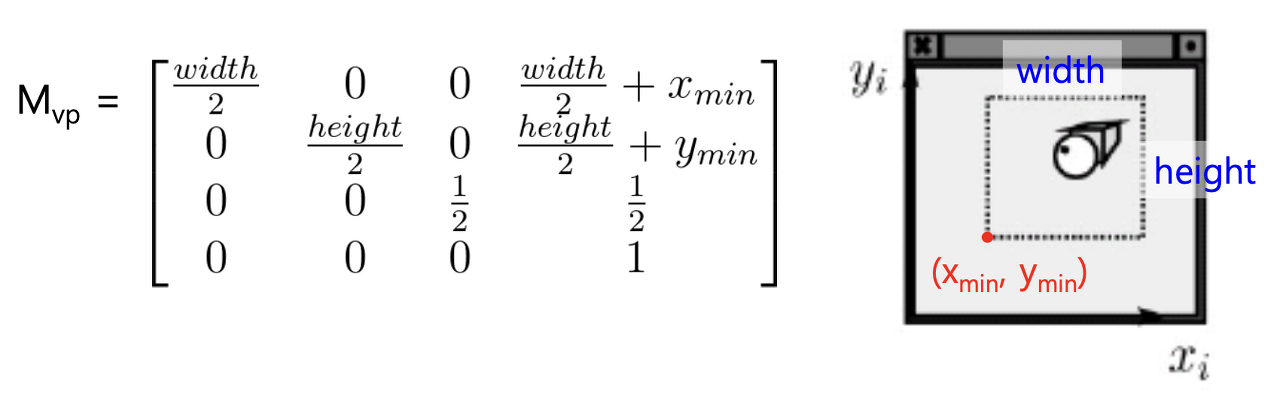
생각해보면 우리는 screen space의 x, y값을 알고 있다. 위 행렬을 곱을 통해 나온 값에 대해 역으로 카메라 좌표계의 x, y값을 구할 수 있다.
이제 방향 벡터를 옮겨야 하는데,.. 방향벡터가 카메라 공간의 projection line이 될 것이고, 이는 한 점에서 시작하고 그 뒤는 원점이 있을 것이다....
원점과 시작점을 잇는다. 시작점은 구했으니 시작점에서 원점을 빼주면 원점에서 시작점으로 향하는 벡터가 나올 것이다.
그리고 이것은 카메라 공간의 방향 벡터가 될 것이다.
* 호모지니어스 좌표에서 w coordinate이 0이면 벡터를 1이면 좌표를 나타낸다. 사실 그래서 시작점에서 w 좌표만 0으로 변경해 주면 된다.
world space에서 camera space로 변환할 때 카메라 좌표를 월드 좌표계의 원점으로 이동하고 로테이션을 하는 변환을 했다. 이제 camera space에서 world space로 변환을 하기 위해선 역행렬을 곱해주면 된다.
[R | t]로 정의한 view matrix를 ray에 적용하면 world space에서 정의가 된다. 이후 world 변환의 역변환을 적용하면 object space의 n개의 ray가 정의된다.
여기까지 object space의 ray를 얻는 과정이다.
'도전' 카테고리의 다른 글
| Normal Mapping (0) | 2023.05.13 |
|---|---|
| Bounding Volumes (0) | 2023.05.13 |
| 3D Computer Graphics (7) (0) | 2023.04.26 |
| 3D Computer Graphics (6) (0) | 2023.04.15 |
| 3D Computer Graphics (5) (0) | 2023.04.15 |

댓글