GPU에 의해서 렌더링이 어떻게 수행되는지 알아보고 그중에서 View transform에 대해 조금 더 알아보자.
우선 GPU Rendering Pipeline은 다음과 같이 구성되어 있다.
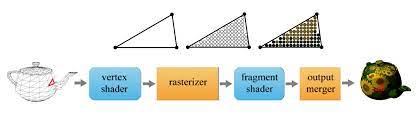
Polygon mesh의 정점들은 vertex array에 저장이 되어있다. 이러한 정점들을 vertex shader가 병렬적으로 한 번에 하나씩 처리하면서 다양한 연산이 적용된다.
그 이후 각 정점의 정보를 사용해 Rasterizer 과정을 거친다. 이 과정에서 삼각형을 재조립한 이후 각 삼각형의 내부 픽셀의 색상을 결정할 정보를 각 픽셀마다 저장하는 작업을 거친다. 이 과정을 하드웨어를 통해 이루어진다. 이를 fragment라고 한다.
이 픽셀에 저장된 정보를 가지고 fragment shader가 각 픽셀의 색상을 결정하고 output merger가 색상을 렌더링 여부와 view를 결정하여 스크린에 보여준다.
transform
3D 그래픽스에서, World transform, View transform, 그리고 Projection transform은 각각 다른 역할을 합니다.
이들은 모두 3D 모델을 2D 화면에 렌더링할 때 사용되는 변환(transform) 중요한 요소입니다.
World transform
World transform은 3D 모델의 좌표를 월드 좌표계(World coordinate system)에서 다른 좌표계로 변환하는 과정입니다.
즉, 모델의 좌표를 원하는 위치, 방향, 크기로 이동하거나 회전시키는 것입니다. 이 변환을 적용하면 3D 모델이 원하는 위치와 방향으로 이동하거나 회전할 수 있습니다.
3D 모델러가 만든 3D 모델은 object space 공간에 위치하게 됩니다.
이를 우리가 world에 배치를 하기 위해선 당연하게 각 모델들을 이동시켜야 하는데 이때 우리는 강체 변환과 비강체변환을 사용하게 됩니다.
보통 강체 변환은 모델의 이동을 다룹니다. translate, rotate 등이 있고 비 강체변환은 모델의 크기를 키우는 scale 등이 있습니다.
이러한 world transform을 통해 world space를 정의하게 됩니다.
View transform
View transform은 월드 좌표계에서 카메라 좌표계로 변환하는 과정입니다.
이 변환을 통해 카메라는 월드 좌표계에서 모델을 볼 수 있는 위치로 이동하게 됩니다.
View transform은 카메라의 위치, 방향, 시야각 등을 설정하는 데 사용됩니다.
카메라로 이를 찍는 다는 것은 카메라도 position이 존재합니다. 3차원 벡터를 가지는 이 카메라는 방향이 있습니다.
어디를 보고 어디까지 찍고 어떤 종횡비를 가질지 , 카메라의 위를 향하는 방향벡터 등등의 정보가 필요합니다.
camera space 는 {u, v, n, EYE}로 만들어집니다.
EYE는 카메라의 위치를 말합니다.
n는 카메라가 바라보는 정점의 위치에서 eye position 바라보는 벡터이며, 이를 단위 벡터로 만듭니다.
u는 카메라의 위를 향하는 벡터와 n간의 외적을 구한 이후 단위 벡터로 만듭니다.
v는 n과 u를 외적을 통해 n, u 벡터에 수직인 벡터를 구합니다.
기존 n과 u 벡터가 이루는 평행사변형의 면적과 n, u 외적의 값이 같기 때문에 v는 별도의 정규화 과정은 필요가 없다.
이렇게 구해진 u, v, n 은 orthonormal basis가 만들어집니다.
* orthonormal basis : 직교 정규 기저, 서로 수직이며 크기가 1인 벡터의 집합.
EYE는 카메라의 중심 원점이고, EYE를 기준으로 u, v, n을 통한 새로운 좌표계가 성립됩니다.
이를 camera space라고 합니다.
그럼 하나의 의문점이 생긴다. world 좌표계에 있는 모델의 좌표와 카메라 좌표계에 있는 모델의 좌표가 서로 다르다는 점이다.
world space 그대로 처리를 하게 되면 rendering 하는 것이 매우 어려워진다.
그래서 이를 camera space로 옮기는 작업을 진행하는데, 이는 렌더링 알고리즘을 개발하는데 더욱 쉬워진다.
그래서 우리는 View Transform을 적용하는 것이다.
어떻게 적용할까?
이를 위해서 translation을 진행해야 한다.
카메라 공간에서의 이동 변환 행렬은 원래의 좌표계를 카메라가 위치한 좌표계로 변환하는 것입니다.
이 변환은 세 가지 변환이 결합된 결과로 구성됩니다
변환된 좌표를 원점 기준으로 이동시키는 변환, 이동된 좌표를 카메라가 위치한 좌표계로 변환하는 변환, 카메라가 위치한 좌표계에서 원래의 좌표계로 변환하는 변환입니다.
이 중에서 첫 번째 변환인 이동 변환은 다음과 같이 표현됩니다.
\begin{bmatrix}1 & 0 & 0 & -eye_x \\0 & 1 & 0 & -eye_y \\0 & 0 & 1 & -eye_z \\0 & 0 & 0 & 1\end{bmatrix}
위의 행렬은 x, y, z 축 방향으로 각각 $-eye_x$, $-eye_y$, $-eye_z$만큼 이동시키는 변환입니다.
이 변환은 원래의 좌표계를 카메라가 위치한 좌표계로 이동시키는 데 사용됩니다.
두 번째 변환은 원래의 좌표계에서 카메라가 위치한 좌표계로 변환하는 변환이며,
이 변환은 카메라가 어떻게 회전되어 있는지에 따라 결정됩니다.
카메라의 회전 변환은 보통 쿼터니언(quaternion)을 사용하여 표현되며, 쿼터니언을 행렬로 변환하여 이동 변환 행렬과 결합하여 사용됩니다.
이를 통해 camera space의 u, v, n 좌표와 world space의 x, y, z를 완전히 일치시키도록 변환시킵니다.
이는 u, v, n을 행으로 만든 행렬을 만들면 된다. (Inverse Rotation)
세 번째 변환은 카메라가 위치한 좌표계에서 원래의 좌표계로 변환하는 변환이며,
이는 첫 번째 변환의 역변환이므로 다음과 같이 표현됩니다.
\begin{bmatrix}1 & 0 & 0 & eye_x \\0 & 1 & 0 & eye_y \\0 & 0 & 1 & eye_z \\0 & 0 & 0 & 1\end{bmatrix}
따라서, 이동 변환과 회전 변환을 결합하여 사용하면, 카메라 공간에서의 변환 행렬을 구할 수 있습니다.
서로의 축이 모두 일치하게 되면 월드 공간과 카메라 공간이 같기 때문에 월드 공간 좌표계와 카메라 좌표계
의 좌표가 동일해진다.
Projection transform
Projection transform은 3D 모델을 2D 화면에 투영하는 과정입니다.
이 변환은 월드 좌표계에서 카메라 좌표계로 이동한 모델을 2D 화면에 투영하는 것을 의미합니다.
이때, 화면에 투영되는 시야각과 종횡비 등이 중요한 요소가 됩니다.
이 세 가지 변환(transform)을 적용하여 3D 모델을 2D 화면에 렌더링 할 수 있습니다.
이렇게 변환된 3D 모델은 그림자, 조명 등의 효과를 추가하여 실제감 있는 이미지로 완성됩니다.
'도전' 카테고리의 다른 글
| 3D Computer Graphics (7) (0) | 2023.04.26 |
|---|---|
| 3D Computer Graphics (6) (0) | 2023.04.15 |
| 기억장치와 PLD(2) (0) | 2023.04.04 |
| 기억장치, PLD (1) (0) | 2023.04.02 |
| 3D Computer Graphics (2) (0) | 2023.04.01 |


댓글