2023.04.02 - [도전] - 기억장치, PLD (1)
기억장치, PLD (1)
알아볼 것. 기억장치의 종류와 특성 RAM, ROM의 내부 구조 및 동작원리 PLD의 구조 및 동작원리 (2) 기억장치. 처리할 프로그램과 데이터를 기억하거나, 처리한 후의 결과를 기억을 하는 장치이다.
chinggin.tistory.com
PLD
프로그램이 가능한 전자 퓨즈선으로 연결된 게이트의 배열로 구성된 집적회로이다.
디지털 시스템의 설계를 위해 PLD를 사용합니다.
PLD를 이용하게 되면 복잡한 논리회로를 하나의 직접회로로 프로그래밍할 수 있어 필요한 소자들의 수와 비용을 절감할 수 있는 장점이 있습니다.
주로 AND 게이트와 OR 게이트의 배열 구조를 갖는 집적회로입니다.
결국 PLD는 논리요소들이 배열 행태로 되어 있어 배열 형태의 내부 연결선을 프로그래밍할 수 있다.
퓨즈선의 연결 유무의 의해 AND-OR 연산을 하며 이를 곱의 합 형식의 조합논리회로가 구현된다.
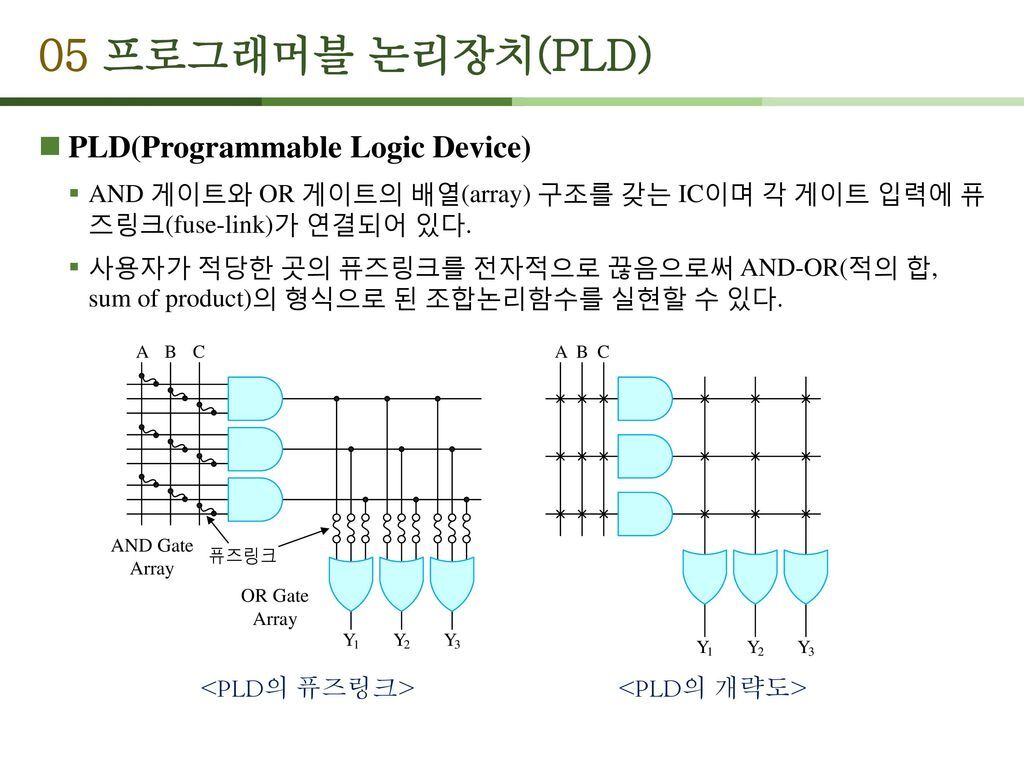
설계자가 퓨즈링크를 어떻게 설계할지에 따라 프로그래밍을 할 수 있다.
PLD의 종류
크게 세 가지의 형태가 있다.
PROM
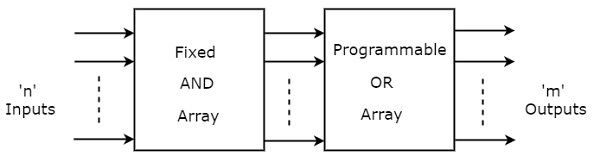
PROM은 논리합에 대한 프로그래밍은 가능한다. AND 게이트의 배열은 프로그래밍하지 못하지만 OR 게이트의 배열은 프로그래밍이 가능하다.
PLA

PLA는 AND 배열과 OR 배열전부 프로그래밍이 가능하다.
ROM과 같은 기능을 수행하며, ROM의 단점을 해소하려고 만들어 졌다.
ROM을 이용해 조합논리회로를 설계한다면 ROM의 크기는 입력의 수에 의해 결정되므로 입력의 수가 많고 사용되는 단어
의 수가 적을 때는 많은 기억공간이 낭비된다.
그러나 PLA는 모든 입력변수를 디코딩하지 않고, 모든 최소항도 만들지 않는다.
PLA의 크기는 입력의 수, 곱항의 수(k Word Lines), 출력의 수로 결정이 된다.
n개의 변수를 갖는 m개의 부울함수를 구현이 가능하다.
1.구현할 때는 조합논리회의 논리를 나타내는 PLA 프로그래밍 표를 작성하고(퓨즈)
2. 작성된 프로그래밍 표를 사용하여 PLA를 제작한다
PLA는 곱의 합 형태로 함수가 표현되기 때문에 곱항의 수를 줄여야 한다. 한정된 수의 AND 게이트를 갖기 때문인데,
이를 도표를 이용하여 간소화한다.
곱항의 수가 최소인 부울함수를 선택하고 선택된 곱항을 이용하여 프로그래밍 표를 작성한다.
이때 카르노맵을 사용 하는데 다음 블로그가 설명을 잘해준다.
https://m.blog.naver.com/leeyunghuk1/220958708825
[카르노맵] 카르노맵
카르노맵 이제까지 보신 AND나 OR 게이트들을 사용하여 함수를 회로로 구현할 ...
blog.naver.com

- : 필요없음
1 : 필요함
0 : 보수가 필요함
C : F1의 보수
T : F2의 정상형
PAL
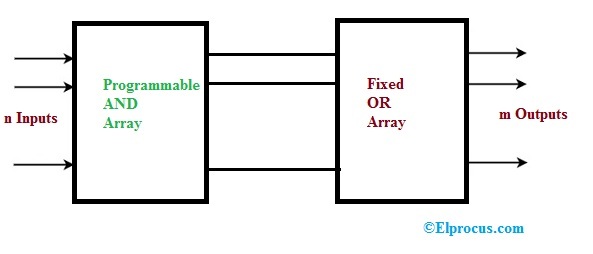
PLA가 가장 융통성이 좋지만 가장 많이 사용하는 것은 PAL이다. PAL은 AND 배열만 프로그래밍 가능하며 OR 배열은 고정되어 있다.
왜 그러냐면 PAL는 구성하는 값이 싸고 논리적으로 구성하기 쉽다고 한다.
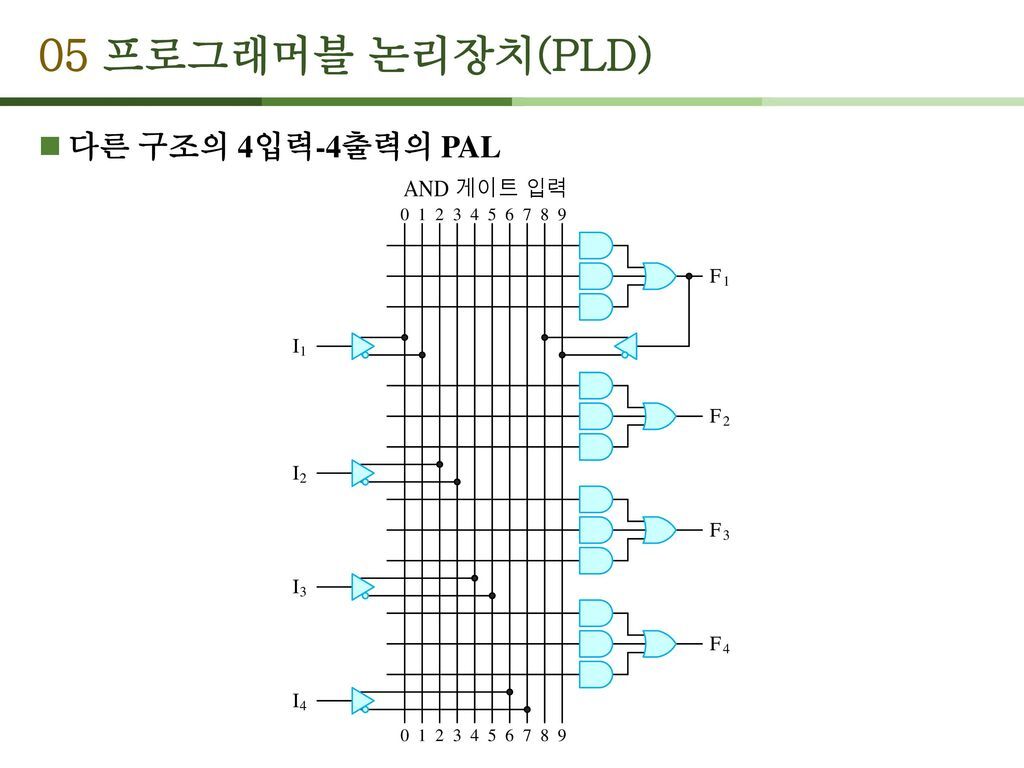
이는 3 AND-OR 구조이다ㅡ 4 입력에 4 출력을 가지는 구조라 할 수 있다.
PLA와 마찬가지로 주호바논리회로를 설계할 수 있다.
도표를 이용하여 부울함수를 간소화한다.
이후 부울함수 중 소거가 가능한 곱항의 수를 가지도록 구성한다.
'도전' 카테고리의 다른 글
| 3D Computer Graphics (6) (0) | 2023.04.15 |
|---|---|
| 3D Computer Graphics (5) (0) | 2023.04.15 |
| 기억장치, PLD (1) (0) | 2023.04.02 |
| 3D Computer Graphics (2) (0) | 2023.04.01 |
| 3D Computer Graphics (1) (0) | 2023.04.01 |



댓글