high frequency polygon mesh를 렌더링 할 때 매우 표면적으로 음영이 드러나 굴곡을 표현하는 것을 볼 수 있다.
사실 이 high frequency는 매우 많은 버텍스를 사용함으로 인해 더 세세하게 표현되는데, 이 약간 울퉁불퉁한 이러한 재질을 어떻게 표현할까?
점 광원이 있다고 하고 각 버텍스에서 점 광원까지의 라이트 벡터를 설정하자.
이 중 난반사를 보면 각 버텍스의 노멀벡터와 라이트 벡터의 각도로 표현할 수 있다.
이를 각 폴리곤 메시의 버텍스에 빛의 세기를 표현하면 오돌토돌한 음영을 만들어 낼 수 있다.
그런데 이렇게 하면 고품질은 되지만 성능과 시간 투자가 많이 필요하다.
그렇다고 이미지 텍스처를 매핑하고 버텍스를 줄이자니 매우 밋밋한 표면이 만들어질 것이다.
시간도 적게들이고 고품질을 표현하는 방법이 없을까? 이 방법이 바로 Normal Mapping이다.
고주파 매시의 노말 벡터만 따와서 이미지 텍스처에 이러한 노말 벡터를 적용을 해보자.
이러한 노말 벡터를 저장하고 있는 텍스처를 우리는 Normal map이라고 부른다.
그리고 실제 렌더링에는 매우 간단한 메시를 사용하여 이를 텍스처에 매핑하면 적은 시간과 적은 성능을 통해 고주파 메시를 표현할 수 있게 된다.
원래 평평하고 간단한 메시를 쓰면 각 버텍스간의 노말 벡터가 동일하게 되는데, 이를 Normal map을 통해 각 버텍스의 노말 벡터를 변경하는 것이다. 이로 인해 광원으로부터 받는 빛의 세기를 표현할 수 있게 된다.
그럼 이를 어떻게 사용할 수 있을까?
우선 노말 맵을 만들어야 할 것이다.
이를 위해선 Height Map이라는 것이 필요하다. Height map은 높이 값을 저장한 텍스처이다.
고주파 메시를 통해 height map을 만들 수 있지만 대게 이미지의 rgb값의 평균으로 height map을 만들어 사용한다고 한다. 몇몇 보정작업은 디자이너가 한다.
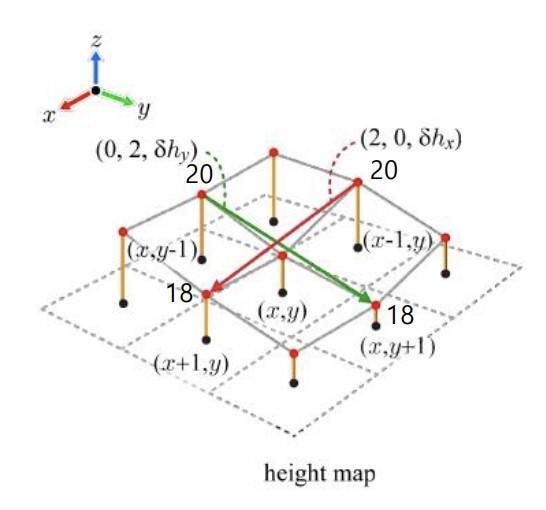
height field의 표면의 기울기를 반영하는 노멀을 저장해야 하는데 이를 위해 샘플링된 중점을 x, y라 해보자.
x, y의 전후방향으로 각각의 점을 잇는다. 점선으로 표현된 선이 바로 전후의 점을 이은 벡터이다.
두 벡터를 외적 하여 수직인 벡터를 얻는다. 이는 height field의 노말을 대략 계산해 낼 수 있다.
계산과정은 곡면의 한 점에서 각 x, y로 편미분을 하여 tan 벡터를 얻고 이를 외적 하여 노멀을 구한다. 근데 이것은 height map에서는 불가능하다. 그래서 앞뒤의 샘플링된 정점을 이어 이를 tan vector로 취급하여 계산하는 것이다. 그래서 실제 노말값을 대략 계산한다고 하는 것이다.
근데 실제론 노멀 벡터를 구하는 방법은 매우 여러 가지가 있다.
이러한 각 중점의 노멀값을 외적으로 구한 값들을 텍스처의 크기에 맞게 전체적으로 구한 뒤 이를 RGB 포맷으로 통일시켜야 한다.
이 포맷은 [0,1] 사이이어야 하기 때문에 노말 벡터를 변형시켜야 한다.
이 노말벡터는 단위벡터이기 때문에 -1에서 1 사이에 존재하고 있다.
그렇기에 1을 더해주고 2로 나누어 0과 1 사이의 RGB 포맷으로 변경해 주면 노말 맵이 만들어진다.
그러면 RGB값이 노말벡터의 x, y, z값으로 처리가 된다.

신기하게 노말맵은 B값이 매우 뚜렷하게 보인다. 왜 그럴까?
이는 z좌표가 크다는 것인데, 이는 벡터의 방향이 z좌표 방향이기에 제일 크기 때문이다.
절벽을 생각해 보면 절벽의 끝은 노말벡터가 z좌표를 향할 것이다. 중간은 x나 y좌표를 향하고 절벽 밑은 z좌표를 향하는 벡터가 있을 것이다.
이러한 x, y방향을 가리키는 벡터보단 z좌표 방향의 벡터가 훨씬 많기 때문에 이를 표현하는 z좌표의 B값이 상대적으로 많고 크기 때문이다.
이제 이를 이용하여 렌더링 과정에는 어떻게 노말 맵을 사용하는지 다음시간에 알아보자.
'도전' 카테고리의 다른 글
| Hellow WebGPU (0) | 2023.05.15 |
|---|---|
| Normal Map (2) (0) | 2023.05.13 |
| Bounding Volumes (0) | 2023.05.13 |
| 3D Computer Graphics (8) (0) | 2023.04.29 |
| 3D Computer Graphics (7) (0) | 2023.04.26 |

댓글